Debarghya Das, A computer hacker in India, uncovers a huge discrepancy in the Indian High School Assessment Exams by analyzing data the same way I do.

Basically, he hacked into the database with the original intention of writing to them and offering them his services on how to fix the security holes. After obtaining the data however, he couldn’t help himself in running some statistical analysis.
It all started with simply plotting a frequency histogram, sometimes called probability distribution chart, what most people call the elusive “Bell Curve.”
This is what all the subjects overlayed look like:
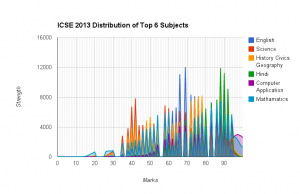 Note: Those peaks and valleys should be a smooth “bell” shape, not jagged spikes as they appear here.
Note: Those peaks and valleys should be a smooth “bell” shape, not jagged spikes as they appear here.
It’s my job to look into unwanted, suspicious, and badly performing data. If this isn’t odd, I don’t know what is. Debarghya suggests this is evidence of tampering with the results. I assume nothing, but I can’t help feeling he may unfortunately be correct. What I know for certain is however illegal this is, it definitely merits some sort of commendation, and most certainly a follow up and response.
Corruption in India is not news, but potential corruption of this grandeur should really warrant some investigaton.
Source article: http://deedy.quora.com/Hacking-into-the-Indian-Education-System

Actually, this abnormality in data for exam results could be possible. Distribution is jagged since question papers do have questions with only 1 points. Its like having coins/currencies in your pocket. even if you take thousands and thousands of samples, you wont get few numbers in your distribution. This can be simulated…. I will try monte carlo simulation and revert back soon if my hypothesis holds
Cheers,
Vinay Thakur
Research Professional
vpsthakur@gmail.com
that’s actually a very interesting point, and I initially had the exact same concern. I said “what about tests with 50 questions, of course you’ll only see every other score…” That didn’t seem odd to me, BUT if you look closely at the data you’ll see the numbers actually come in very specific increments, namely, in increments of 1, 2, 3, 4, 5, AND 6 (consecutively, as a matter of fact). With those 6 increments alone, every single number from 1-100 is theoretically achievable, read the source link and Debarghya does a great job of explaining in more detail.
if the distribution is not normal, is it not possible that number of students appearing for exams are really less for Central Limit Theorem to hold ?
Same here this distribution is not normal..
Preschools in Bengaluru